
Research
Research interest in the fields of causation, fundamental AGI, living systems, semantical SETI, and the design of theory and methods to navigate software space
-

Remodelling machine learning: An AI that thinks like a scientist
This video produced by Nature on their own initiative, shows our AI approach to scientific causal discovery to find the underlying algorithmic models that interact and generate data to help scientists uncover the dynamics of cause and effect.

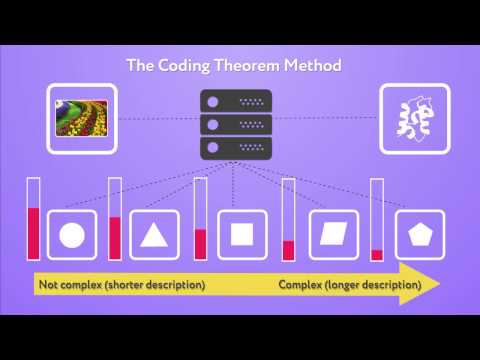
Algorithmic Information Dynamics: A Discrete Calculus to Navigate Software Space
A discrete calculus in software space that combines algorithmic complexity and perturbation analysis to navigate between the physical world and software space (as in the Matrix) to conduct guided searches (in the space of all computer programs) so as to reveal computable (generative and mechanistic) models.

Signal Deconvolution of Extraterrestrial Messages
This video explains how our research on the semantics of SETI can help decipher the meaning of messages. We show that non-random data encodes its spatial, geometrical, and topological properties.

Steering and Reprogramming Life
We introduce a discrete-calculus and framework to manipulate and study interventions for causal analysis in application to dynamical systems, adaptive complex and living systems based upon the theory of algorithmic information that takes into account the causal history of an evolving system over time.


Reprogrammable World - Algorithmic Nature Lab
Introduction to the theory and methods of asymptotic statistical evidence of Turing universality, the application of which has led to evidence suggesting pervasive computational universality among the space of all computer programs and perhaps in the real physical world by extrapolation of evidence of computation (e.g. the fact we can build digital computers)

Graph Complexity
The introduction of a native multi-dimensional resource-bounded measure of algorithmic complexity based on n-dimensional models of computation to measure complexity from vectors to matrices (e.g. 2D images) and tensors (e.g. isomorphic graph groups).

Algorithmic Cognition
The introduction of an ‘inverse Turing test’ experiment with more than three 3K humans proving that cognitive evolution can be captured by our resource-bounded index. The results were generalised to several landmark animal and insect experiments.

Algorithmic Information Dynamics MOOC - intro video
Algorithmic Information Dynamics (AID) is an observer-oriented theory and methodological framework for causal discovery and causal analysis based on the principles of the theory of algorithmic information and perturbation analysis.
Universal Measures of Complexity - Algorithmic Nature Group http://complexity-calculator.com/
The introduction of a divide-and-conquer resource-bounded measure based upon and inspired by algorithmic probability. It has enabled, for the first time, an estimation of an empirical distribution of the so-called Universal Distribution or Levin’s semi-measure on different computing models.
Key foundational concepts explained by an award-winning computable slice image of the uncomputable space

This picture, titled “Visualising the Computational Universe: Runtime Space in a Peano Curve,” won me 1st. prize in the Computational Imagery category of the “2011 Kroto Institute Scientific Image Competition” held in the UK. Here is the explanation: It represents a small slice of the computational universe of all possible computer programs.
Each pixel represents a computer program with empty input running on an abstract computer (a Turing machine). The color indicates the runtime of the program upon completion of its computation. The darker a pixel the longer the program took to produce its output. White pixels are computer programs that do not produce any output because they never halt (just as happens when your computer stalls forever, sometimes making you reboot).
Red pixels are the computer programs that take the longest time—relative to other programs of the same size—before finishing (they are also called Busy Beavers). I call this color type coding the computability spectrum. Programs were sorted by size from smallest to largest (in terms of number of instructions) in such a way that one could be certain that any program would eventually be reached (including versions of MS Windows and Angry Birds that can be encoded as one-run computer programs).
Because there is no upper limit to the size of programs, the space of all computer programs is infinite but discrete, perhaps mirroring our own world. Because an enumeration of computer programs is linear (you start with program 1, then proceed to program 2, and so on) pixels depicted in this 2-dimensional figure are disposed along a “space-filling” Peano curve. This is a curve that guarantees that 2 contiguous elements in the enumeration remain as close as possible to each other in the 2D configuration.
The picture has the striking particularity that it is ultimately uncomputable. Imagine you point a telescope and take a picture of an object in the computational universe for which some pixel values cannot be determined, not only in practice but in principle– that is, no matter how good your camera, or how many ‘terapixels’ some future version of it may have. This slide of the computational universe was only possible because it is a tiny region of small computer programs for which all pixels can be determined by zooming in deep enough.
However, Gödel and Turing proved that if you zoomed out to a larger view of the computational universe, the picture would begin to look completely blurry because pixel colours would not be determinable. In other words, this picture is the inverse equivalent of Hubble’s Deep Field space–the larger the space field the blurrier.
● While we can only have access to the visible universe determined by the speed of light, we can only see a small part of the computational universe due to similar limitations both physical and computational (it seems we cannot build more powerful computers than the ones we already have to overcome these limitations). Hence, most of the computational space will remain unknowable, not only due to a limitation of resources but also due to a fundamental barrier established in the digital world and extending into our own reality.
Only incremental improvements to this picture are possible. While the picture is ultimately uncomputable and unattainable, one can make an informed guess as to what it would look like if zoomed out. The theory predicts the average color of the picture at a greater scale, this theory being the theory of algorithmic probability, closely related to what is known as the Chaitin Omega number, or the halting probability. It turns out that the picture will be mostly white, as in an ever-expanding universe, finding computer programs that halt and produce something will be increasingly harder. Indeed, most programs will never halt, and those that halt will do so relatively quickly in proportion to their size (see paper P10).
Algorithmic probability also tells us that most programs will produce an output following exponential decay (-log_2 Pr(s)) hence most of them will produce the same strings and the fewest will produce algorithmically random digital sequences. In other words, among the computer programs that do produce an output, most of them will be highly ordered, as if they were creating a structured digital universe of highly ordered patterns out of nothing (just like ours). Some of these programs that produce the same output may do so faster than others, but precisely how much faster a program can be is another open foundational question and one of the greatest challenges in mathematics and computer science. If it were possible to find a program considerably faster than any other, then everything could be computed in ‘reasonable’ time, regardless of the apparent difficulty of the computation.
A full technical explanation of some of this and of how the image was generated was published in this paper:
H. Zenil, From Computer Runtimes to the Length of Proofs: With an Algorithmic Probabilistic Application to Waiting Times in Automatic Theorem Proving In M.J. Dinneen, B. Khousainov, and A. Nies (Eds.), Computation, Physics and Beyond International Workshop on Theoretical Computer Science, WTCS 2012, LNCS 7160, pp. 223-240, Springer, 2012.
A preprint is available online here.


